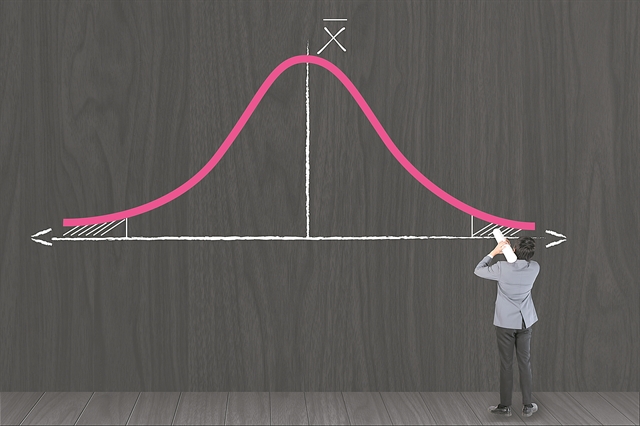
Η κορυφή και τα άκρα της καμπύλης Gauss
Στη σειρά του ΒΗΜΑ-Science για όσους θέλουν να φτιάξουν ξανά τη… σχέση τους με τα Μαθηματικά μαθαίνουμε για τη σημασία της «κωδωνοειδούς καμπύλης» και κάποιες από τις πολλές εφαρμογές της
Στο προηγούμενο τεύχος είδαμε την ιστορική διαδρομή της καμπύλης που μοιάζει με καμπάνα. Αλλοτε πιο πλατιά και άλλοτε πιο συμμαζεμένη, είναι γνωστή ως «κωδωνοειδής καμπύλη», «κανονική κατανομή», «καμπύλη κατανομής συχνοτήτων» αλλά και «Gaussian distribution» ή «bell curve» (αφού bell στα αγγλικά σημαίνει καμπάνα). Η «ανακάλυψή» της πίσω από πολλές συλλογές αριθμητικών στοιχείων και η συνειδητοποίηση για την εμφάνισή της σε τόσες και τόσο διαφορετικές περιπτώσεις τής έδωσαν για πολλά χρόνια πρωταγωνιστικό ρόλο σε αυτό που ονομάζεται στατιστική επιστήμη.
«Αξονική» απεικόνιση
Συνήθως η καμπύλη αυτή παρουσιάζεται με τη βοήθεια δύο κάθετων μεταξύ τους αξόνων. Στον οριζόντιο κατατάσσουμε κάποια γεγονότα και στον κάθετο άξονα είτε την αντίστοιχη πιθανότητα για το κάθε γεγονός είτε έναν αριθμό που εκφράζει τη συχνότητα εμφάνισης του συγκεκριμένου γεγονότος. Γι’ αυτό και η καμπύλη που προκύπτει μπορεί να ονομάζεται και «κατανομή». Δηλαδή το πώς κατανέμονται τα γεγονότα με βάση τη συχνότητα εμφάνισής τους. Ενα χαριτωμένο αλλά διδακτικό παράδειγμα της χρήσης της καμπύλης αναφέρει ο βραζιλιανικής καταγωγής μαθηματικός Αλεξ Μπέλος στο βιβλίο του «Adventures in Numberland». Εχει ήρωα τον διάσημο γάλλο μαθηματικό, φυσικό, μηχανικό και φιλόσοφο Ανρί Πουανκαρέ (1854-1912). Λέγεται ότι ο Πουανακαρέ επί έναν χρόνο καθημερινά ζύγιζε την μπαγκέτα του ψωμιού που αγόραζε από συγκεκριμένο φούρνο, διότι υποψιαζόταν ότι ήταν συστηματικά λιπόβαρη. Στο τέλος του χρόνου ήταν σε θέση να βάλει στον οριζόντιο άξονα τα βάρη που είχαν προκύψει κατά τις ζυγίσεις και στον κάθετο άξονα το πόσες μπαγκέτες είχαν βρεθεί με το αντίστοιχο βάρος. Ετσι δημιουργήθηκε μια «καμπύλη κατανομής» που είχε τη μορφή, τι άλλο, μιας… Gaussian distribution. Αλλά η κορυφή της καμπύλης, που εκεί εγκαθίσταται ο μέσος όρος όλων των μετρήσεων, αποδείχθηκε ότι δεν βρισκόταν ακριβώς στο νόμιμο βάρος της μπαγκέτας αλλά αρκετά γραμμάρια πιο χαμηλά. Και αυτό οδήγησε τον ιδιοκτήτη του φούρνου ενώπιον του νόμου!
Συμμετρία και μέσος όρος
Σε κανονικές καταστάσεις η καμπύλη αυτή παρουσιάζει συμμετρία γύρω από τον μέσο όρο, που αντιστοιχεί στην κορυφή της, και είναι πιο ανοικτή ή πιο κλειστή γύρω από αυτόν ανάλογα με το πόσο μεγάλο ή πόσο μικρό αντίστοιχα είναι το τυχαίο σφάλμα που έχουμε κάνει στις μετρήσεις μας. Αυτή την κατανομή ακολουθούν, για παράδειγμα, το ύψος των παιδιών σε μια τάξη, τα (όχι συστηματικά) λάθη στις μετρήσεις, η μέτρηση της πίεσης του αίματος, η βαθμολογία ενός διαγωνίσματος.
Επίσης τα δύο άκρα της εκεί που πηγαίνουν να συναντήσουν τον οριζόντιο άξονα είναι αξιοπρόσεκτα. Διότι αν είναι αρκετά «παχιά» (fat tailed τα αποκαλούν και οι αγγλόφωνοι), δηλαδή για αρκετό διάστημα όχι πολύ κοντά στον οριζόντιο άξονα, σημαίνει πως ακραία συμβάντα δεν είναι και τόσο απίθανα. Και στο γνωστό και άκρως ευπώλητο βιβλίο-δοκίμιο, μεταξύ άλλων, για την τυφλότητα απέναντι στην τυχαιότητα, του Νασίμ Νίκολας Τάλεμπ, «Ο μαύρος κύκνος», μια από τις βασικές θέσεις του συγγραφέα είναι ότι «τείνουμε να υποτιμούμε τις ουρές στις καμπύλες κατανομής», εκεί όπου συμβαίνουν σημαντικά γεγονότα, όπως η εμφάνιση του Διαδικτύου και η επίθεση στους Δίδυμους Πύργους στις 11.9.2001.
Πνευματική Γυμναστική
- Ζητούνται οι ακέραιοι θετικοί, που αντιπροσωπεύουν τα Μ και Ν ώστε να ισχύει: MN x MM = NMMN. Οι ΜΝ, ΜΜ, ΝΜΜΝ είναι θετικοί ακέραιοι αριθμοί.
- Θέλουμε να βοηθήσουμε έναν φίλο μας να φτιάξει για τον κήπο του 12 λίτρα υδατικό διάλυμα με περιεκτικότητα 25% σε κάποια υγρή ουσία ενώ διαθέτει δύο διαλύματα, το ένα με περιεκτικότητα 30% και το άλλο με 15% από αυτή την ουσία. Δεν θέλουμε να τον μπλέξουμε σε εξισώσεις με Χ και 12 – Χ κ.λπ. Πώς θα του εξηγήσουμε πώς πρέπει να σκεφτεί πρακτικά;
Οι λύσεις των προηγούμενων κουίζ
- Τρεις άνθρωποι μπαίνουν σε ένα σκοτεινό δωμάτιο όπου υπήρχαν 3 μπλε και 2 κόκκινα καπέλα, φορούν από ένα και βγαίνουν στο φως χωρίς να δουν το χρώμα του δικού τους καπέλου. Βγαίνοντας στο φως ο Α κοιτάζει τους άλλους δύο και λέει: «Αραγε τι χρώμα καπέλο φορώ;». Ο Β απαντά: «Ούτε κι εγώ ξέρω για εμένα». Ο Γ που τους άκουσε, αν και πάσχει από αχρωματοψία, λέει αμέσως μετά: «Εγώ ξέρω τώρα τι χρώμα είναι το καπέλο μου». Πώς το ήξερε; Προφανώς ο Α είδε πως οι άλλοι δύο φορούσαν ή ο ένας μπλε και ο άλλος κόκκινο ή και οι δύο μπλε. Μετά, ο Β κοίταξε τον Γ. Αν αυτός φορούσε κόκκινο, ο Β δεν θα μπορούσε να φοράει και εκείνος κόκκινο, άρα θα καταλάβαινε ότι σίγουρα φορούσε μπλε. Ο Γ, αφού τους άκουσε, σκέφτηκε όλα αυτά και, αν και δεν ξεχώριζε χρώματα, κατάλαβε ότι εκείνος φορούσε μπλε.
- Ζητείται ο μικρότερος θετικός ακέραιος αριθμός που όταν διαιρεθεί με το 2 δίνει υπόλοιπο 1, όταν διαιρεθεί με το 3 αφήνει υπόλοιπο 2, με το 4 υπόλοιπο 3, με το 5 υπόλοιπο 4, με το 6 υπόλοιπο 5, με το 7 υπόλοιπο 6, με το 8 υπόλοιπο 7, με το 9 υπόλοιπο 8 και με το 10 υπόλοιπο 9.
Για να αφήνει ένας αριθμός Ν υπόλοιπο π.χ. 6 όταν διαιρείται με το 7 θα πρέπει ο αμέσως επόμενός του, ο Ν + 1 να είναι πολλαπλάσιο του 7. Για παράδειγμα κάντε τη διαίρεση 48 διά 7. Δίνει υπόλοιπο 6 και ο 49 διαιρείται ακριβώς με το 7. Φτιάχνουμε επομένως ο: 2 Χ 3 Χ 4 Χ 5 Χ 6 Χ 7 Χ 8 Χ 9 Χ 10 = 3628800 – 1 είναι ένας αριθμός που θα πληρούσε τις απαιτήσεις με τα υπόλοιπα. Αλλά υπάρχει και μικρότερος. Διότι αν ένας αριθμός διαιρείται με το 2 και το 4 διαιρείται και με το 8. Αν διαιρείται με το 2 και το 5 διαιρείται και με το 10. Αν διαιρείται με το 2 και το 9, επειδή 2 Χ 9 = 18 διαιρείται και με το 6. Αρα και ο αριθμός: 2 x 4 x 5 x 7 x 9 = 2520 αν του αφαιρέσουμε 1, δηλαδή ο 2519, μας κάνει.
Ακολουθήστε το in.gr στο Google News και μάθετε πρώτοι όλες τις ειδήσεις







![Άκρως Ζωδιακό: Τα Do’s και Don’ts στα ζώδια σήμερα [Παρασκευή 18.04.2025]](https://www.in.gr/wp-content/uploads/2025/04/evgeni-tcherkasski-Ap4h8QIxPVE-unsplash-600x401.jpg)














































 Αριθμός Πιστοποίησης Μ.Η.Τ.232442
Αριθμός Πιστοποίησης Μ.Η.Τ.232442