Ανάποδα, σχηματίζοντας με τρίγωνα ή διάφορα πολύγωνα κομμένα σε πολλαπλά χάρτινα κομμάτια που έχουν προκύψει από τετράγωνα ή άλλα κανονικά σχήματα, μπορούν να δημιουργούνται νέα σχήματα που να προσομοιάζουν με ζώα, πρόσωπα, σώματα, κτίρια, δίνοντας πρώτες ιδέες για το πώς επιτυγχάνεται ο σχηματισμός επιφανειών, και στη συνέχεια διαφόρων πλασμάτων, ανθρώπων, ζώων, εξωγήινων κ.λπ. στον υπολογιστή με τη βοήθεια των πολλών μικρών πολυγώνων.
Ο πρωτοπόρος Εσερ
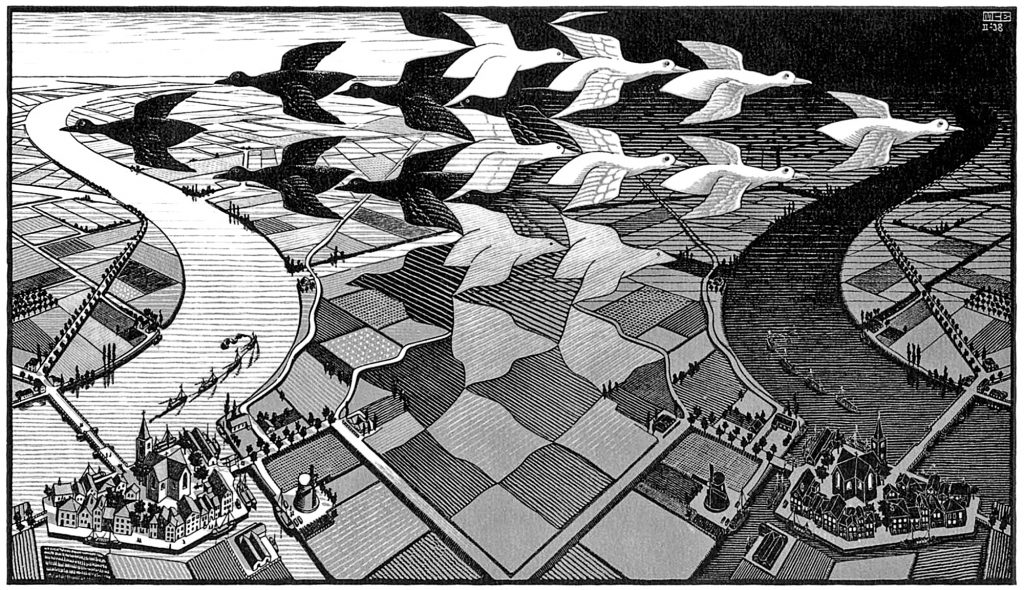
Και το παιχνίδι φουντώνει όταν η τάξη αρχίζει να μιμείται τον Ολλανδό Μάουριτς-Κορνέλις Εσερ (1898-1972), που χωρίς να είναι μαθηματικός άφησε χαρακτικά και πίνακες να σε κάνουν να λες ότι θα πρέπει να έπαιζε στα δάχτυλα τα μαθηματικά των πλακοστρώσεων. Διαβάζοντας όμως περισσότερα για τη ζωή του Εσερ μαθαίνεις ότι έφτασε να έχει αλληλογραφία με τον διάσημο μαθηματικό της εποχής Γκ. Πόλια και να μαθαίνει από αυτόν για διάφορες οικογένειες συμμετριών που δεν τις είχε δει ούτε στα πλακίδια του ανακτόρου της Αλάμπρα.
Μέσα σε ένα τετράγωνο ζωγραφίζονται ένα ή δύο σχήματα (και χωρίς κάποια συγκεκριμένη μορφή), αρκεί να περιλαμβάνουν μέρος ή και ολόκληρη μια πλευρά και αν είναι δύο σχήματα να βρίσκονται σε προσκείμενες πλευρές (όχι απέναντι πλευρές). Κόβονται και προσκολλώνται στις δυο άλλες πλευρές εξωτερικά του αρχικού τετραγώνου. Δημιουργείται ένα πολύπλοκο σχήμα με εμβαδόν όμως όσο του αρχικού τετραγώνου. Αυτό αρχίζουμε και το επαναλαμβάνουμε δημιουργώντας πραγματικά μια πλακόστρωση καλυπτική (δεν αφήνει κενά) που με δυο-τρεις γραμμές και τον κατάλληλο χρωματισμό θυμίζει όμως έντονα Εσερ. Προς μεγάλο ενθουσιασμό των μικρών.
Γνωρίζετε ότι…
Υπάρχουν και στις πολύ απλές πλακοστρώσεις με τετράγωνα πλακίδια προβλήματα κάλυψης της επιφάνειας; Δίνουμε εδώ κάποια επιπλέον προβλήματα για όσους θα έχουν κάπως περισσότερο χρόνο:
1. Σε ένα δάπεδο μπάνιου με 64 τετραγωνικά πλακάκια (8×8) έπρεπε να αφαιρεθούν το επάνω αριστερά γωνιακό πλακάκι και το κάτω δεξιά. Στη νέα πλακόστρωση που θα γινόταν παραγγέλθηκαν πλακάκια κολλημένα δυο μαζί, σχηματίζοντας ορθογώνιο παραλληλόγραμμο. Μπορεί να γίνει η δουλειά (χωρίς να σπάσουμε ούτε ένα);
2. Στο ίδιο δάπεδο, αν πρέπει να λείπει μόνο το επάνω αριστερά γωνιακό και φέρουν πλακάκια που είναι τρία μαζί τετράγωνα κολλημένα σε ένα παραλληλόγραμμο, επιτυγχάνεται η πλακόστρωση (χωρίς να σπάσουμε κάποιο);
‘Εντυπη έκδοση Το Βήμα







![Άκρως Ζωδιακό: Τα Do’s και Don’ts στα ζώδια σήμερα [Δευτέρα 21.04.2025]](https://www.in.gr/wp-content/uploads/2025/04/maarten-verstraete-yoK3oL2Lypo-unsplash-600x375.jpg)



![Δισεκατομμυριούχοι: Οι περιουσίες των κροίσων εν μέσω της μεγάλης κόντρας για τους δασμούς [γράφημα]](https://www.ot.gr/wp-content/uploads/2025/04/ot_bloomberg_billionaires_25-300x300.png)



















![Άκρως Ζωδιακό: Τα Do’s και Don’ts στα ζώδια σήμερα [Δευτέρα 21.04.2025]](https://www.in.gr/wp-content/uploads/2025/04/maarten-verstraete-yoK3oL2Lypo-unsplash-315x220.jpg)






















 Αριθμός Πιστοποίησης Μ.Η.Τ.232442
Αριθμός Πιστοποίησης Μ.Η.Τ.232442